Apprenez À Calculer Le Point De Rencontre Entre Deux Droites Grâce À Des Méthodes Simples Et Efficaces. Maîtrisez L’art De Déterminer Ce Point Crucial.
**méthodes Pour Trouver Le Point D’intersection**
- Comprendre Les Concepts Fondamentaux D’intersection
- Méthode Graphique : Visualiser Les Solutions
- Le Calcul Algébrique : Une Approche Systématique
- L’utilisation Des Logiciels Pour La Résolution
- Applications Pratiques Dans La Vie Quotidienne
- Erreurs Communes À Éviter Lors Des Calculs
Comprendre Les Concepts Fondamentaux D’intersection
Dans le domaine des mathématiques, le concept d’intersection revêt une importance fondamentale, notamment dans la résolution de problèmes impliquant des équations. Au cœur de cette notion, on retrouve l’idée de trouver les valeurs communes entre différentes cartes représentant des relations. Cela peut être visualisé comme deux routes qui se croisent ; les coordonnées de ce croisement représentent les solutions aux équations. Dans un sens plus large, cela nous permet de comprendre comment deux ou plusieurs ensembles se rejoignent, une compétence précieuse, tant dans le monde académique que dans la vie quotidienne.
Pour appréhender cette idée plus en profondeur, il est indispensable d’apprendre le langage des équations. Chaque équation peut être perçue comme une directive (Sig) qui guide vers une solution. En analysant des équations linéaires ou quadratiques, par exemple, nous découvrons des méthodes différentes pour établir ce point d’intersection. L’utilisation d’outils graphiques nous aide à donner vie à ces concepts, rendant l’apprentissage interactif et engageant. De plus, en examinant comment deux fonctions peuvent se rencontrer, on ne se contente pas de résoudre un problème mathématique, mais on développe également la capacité à penser de manière critique.
En appliquant ces connaissances à des scénarios de la vie réelle, tel que le réglage de nos priorités ou la gestion du temps, nous pouvons identifier des moments culminants qui nous permettent de maximiser notre efficacité. Qu’il s’agisse d’une “Pharm Party” où les gens échangent des conseils sur les “Happy Pills” ou de la manipulation de “Fridge Drugs”, la capacité à décoder et à gérer ces intersections peut être cruciale. En fin de compte, acquérir une compréhension approfondie des points d’intersection aide à naviguer dans les complexités de tant de domaines.
| Concept | Description |
|---|---|
| Intersection | Point où deux ou plusieurs lignes/ensembles se rencontrent. |
| Equations Linéaires | Formes d’équations dont les graphiques sont des lignes droites. |
| Coordonnées | Valeurs numériques qui aident à localiser un point sur un graphique. |
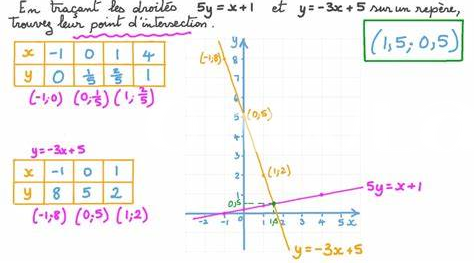
Méthode Graphique : Visualiser Les Solutions
La méthode graphique est une approche intuitive et visuelle pour déterminer le point de rencontre entre deux droites. En traçant ces droites sur un graphique, nous pouvons facilement observer leurs intersections. Pour ce faire, il est essentiel d’établir les équations des droites courbes, souvent sous forme de y = mx + b, où m représente la pente et b l’ordonnée à l’origine. En utilisant un papier millimétré ou un logiciel, on peut obtenir une représentation claire. De cette manière, le processus devient similaire à une prescription médicale : savoir combiner les bons éléments peut mener à un résultat optimal.
Visualiser les solutions permet non seulement d’identifier rapidement les points d’intersection, mais également de comprendre l’impact des variations sur l’angle et la position des droites. C’est un peu comme suivre les directions sur une prescription (Sig) pour atteindre un objectif de santé. Si les droites sont parallèles, il est facile de conclure qu’aucune solution n’existe. D’autre part, si elles se croisent, cela représente une solution unique, et toutes ces informations peuvent être comparées à un Med Rec où chaque détail compte pour une compréhension globale.
Enfin, cette méthode peut être grandement facilitée par des outils numériques qui offrent la possibilité de tracer des droites avec précision. Les graphes interactifs peuvent tenir compte de multiples facteurs, tout comme un pharmacien utilise une base de données pour vérifier les interactions médicamenteuses. Ce type de visualisation transformera votre analyse en une experience plus dynamique et accessible, permettant de résoudre des problèmes mathématiques de manière engageante, tout en évitant le stress d’une Pharmageddon au moment où l’on doit effectuer des calculs complexes.
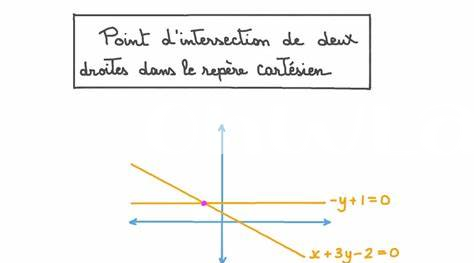
Le Calcul Algébrique : Une Approche Systématique
Le calcul algébrique est un outil puissant qui permet de déterminer le point de rencontre entre deux droites de manière systématique. En utilisant des équations, nous pouvons traiter différentes situations géométriques avec précision. Prenons, par exemple, l’équation de deux droites : l’une peut être exprimée sous la forme y = mx + b, tandis que l’autre pourrait suivre une formule parallèle. En les égalant, nous créons un système d’équations qui nous aide à identifier le point d’intersection.
Pour résoudre ce système, une approche courante consiste à isoler une variable et substituer dans l’autre équation. Cela peut sembler compliqué, mais c’est similaire à compter et verser les médicaments dans le cadre d’une prescription. Chaque étape, tout comme dans la prescription, doit être soigneusement suivie pour garantir que le résultat soit correct. Ce processus systematic peut être très satisfaisant, car chaque étape permet de vérifier la validité de nos solutions.
Un autre aspect crucial de l’algèbre est la vérification des solutions. En mais utilisant la substitution inverse, nous pouvons rapidement montrer que le point trouvé correspond bien aux équations originales. Cela ressemble à un contrôle de médication, où une vérification minutieuse est essentielle pour le bien-être du patient. Ignorer cette étape peut entraîner des erreurs, tout comme dans un environnement pharmaceutique, où des erreurs de dosage peuvent avoir des conséquences graves.
Finalement, le calcul algébrique ne se limite pas simplement à résoudre des équations ; il ouvre un monde de possibilités dans la représentation graphique et la modélisation. Pour ceux qui ne sont pas familiers avec ces méthodes, la complexité peut sembler intimidante, mais avec de la pratique, tout devient plus clair. En somme, comprendre cette approche vous permettra d’acquérir des compétences pratiques applicables non seulement en mathématiques, mais aussi dans d’autres domaines de la vie quotidienne.
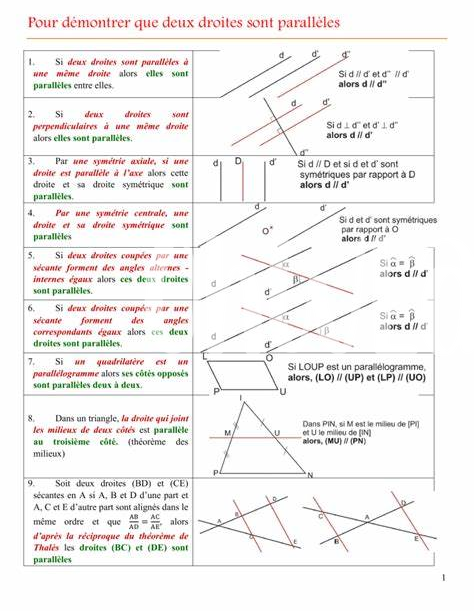
L’utilisation Des Logiciels Pour La Résolution
Dans le monde moderne, l’intégration de la technologie a révolutionné la manière de trouver le point de rencontre entre deux droites. De nombreux logiciels disponibles aident à visualiser les graphiques et à résoudre des équations de manière instantanée. Ces outils permettent de transformer des calculs complexes en représentations visuelles, rendant ainsi accessible la compréhension des intersections. On peut ainsi afirmer que ces applications agissent comme une sorte d’élixir, offrant une solution sucrée à des problèmes mathématiques parfois amers.
L’utilisation d’applications dédiées permet d’automatiser le processus de calcul algébrique. Par exemple, avec des programmes comme GeoGebra ou des tableurs avancés, il est possible d’importer des équations et d’obtenir visiblement les points d’intersection. En quelques clics, vous pouvez passer du rêve à la réalité mathématique sans avoir à vous plonger dans des calculs fastidieux. Cela est particulièrement utile pour les étudiants qui cherchent à comprendre les principes fondamentaux derrière les lignes et les intersections, tout en rendant le tout beaucoup plus engageant.
Enfin, l’intégration de ces logiciels dans des contextes pratiques, tels que des projets scolaires ou des applications réelles, fait briller davantage leur pertinence. Ils évitent ainsi les erreurs communes qui peuvent survenir lors des calculs manuels. Par exemple, une simple faute de frappe ou une confusion dans les étapes peut mener à une mauvaise résolution. C’est là que la technologie, à travers ces outils, peut jouer un rôle crucial, permettant non seulement d’acquérir des compétences, mais aussi de réussir avec brio dans le domaine des mathématiques.
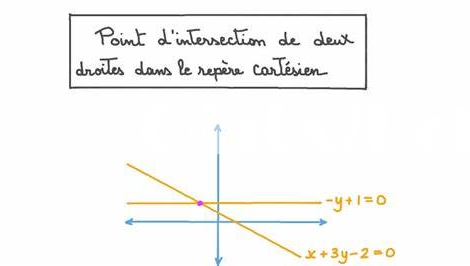
Applications Pratiques Dans La Vie Quotidienne
Dans la vie quotidienne, comprendre le point de rencontre entre deux droites peut sembler un concept mathématique complexe, mais ses applications sont bien plus simples qu’il n’y paraît. Prenons l’exemple d’une situation où vous planifiez un budget. En traçant vos revenus et vos dépenses sur un graphique, le point d’intersection représente la situation où vos dépenses égalent vos revenus. Cela vous aide à visualiser si vous devez réduire vos dépenses ou augmenter vos revenus pour éviter un déficit. Ainsi, cette méthode vous permet de prendre des décisions éclairées concernant vos finances.
Un autre domaine où la compréhension des intersections est cruciale est dans la pharmacie. Lorsqu’un professionnel de la santé prescrit des médicaments, il faut tenir compte des interactions possibles entre ceux-ci. Ici, l’analogie de l’intersection prend toute sa signification : il est essentiel de rechercher des points d’intersection entre les indications, les effets secondaires et les contre-indications. Cela aide à prévenir des scénarios où des médicaments pourraient aggraver des conditions préexistantes ou engendrer des effets indésirables, assurant ainsi la sécurité des patients.
En outre, pensez à l’application des concepts de point d’intersection lors de l’organisation d’événements. Par exemple, lorsque vous planifiez une fête, vous pouvez utiliser des tableaux d’invités pour voir où les préférences de chacun se croisent. Une fois que vous avez identifié ce point de rencontre, vous pourrez créer des activités qui plairont à tous. Voici un tableau représentant différents scénarios d’applications pratiques dans des contextes variés.
| Scénario | Point d’Intersection | Résultat |
|---|---|---|
| Budget personnel | Dépenses = Revenus | Équilibre financier |
| Prescriptions médicales | Interactions des médicaments | Sécurité du patient |
| Planification d’événements | Préférences des invités | Activités inclusives |
Erreurs Communes À Éviter Lors Des Calculs
Lors de la recherche d’un point d’intersection, il est crucial d’être vigilant afin d’éviter des erreurs fréquentes qui peuvent compromettre les résultats. Une des principales fautes survenant est de négliger de bien définir les équations avant de procéder aux calculs. Cela peut être comparé à un “syndrome d’écriture” où les détails essentiels sont omis, résultant en une intersection erronée. Pour illustrer, s’il arrive que la forme d’une équation ne soit pas correcte, on pourrait se trouver à faire des calculs sur une base qui n’est pas solide, tel un “candy man” prescrivant sans examiner adéquatement.
Un autre piège à éviter est de ne pas vérifier la précision des calculs intermédiaires. Comme lors d’une distribution de médicaments, une petite erreur dans les dosages peut mener à des résultats désastreux. L’hésitation à vérifier chaque étape peut créer une spirale de confusions. En effet, c’est en s’assurant que chaque étape soit exacte, tout comme un “pharm tech” vérifiant les prescriptions, que l’on peut garantir une solution fiable.
Enfin, il est essentiel de prendre le temps nécessaire pour relire et valider le travail effectué. Le manque de temps pour un “quality check” peut mener à des erreurs fatales. Tout comme dans un environnement pharmaceutique où une prescription doit être sérieusement contrôlée avant d’atteindre le patient, chaque étape de calcul doit être minutieusement examinée. En somme, la rigueur et l’attention aux détails sont vitales pour réussir dans cette démarche Mathématique.